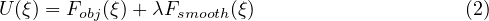2020/04/26ロボットの動作計画における最適化

本ページでは，これまでに日本ロボット学会誌に掲載された解説記事の中から注目度の高い記事をHTML形式で紹介しています．HTMLへの変換時に著者紹介，キーワードなど一部の情報は省略しています．また，レイアウトはオリジナル記事とは異なります．

PDF形式のオリジナル記事はこちらでご覧になれます．引用する際は，本Webページではなくオリジナル記事を引用してください．

---

1 緒言

従来より，何らかの評価関数に従ってロボットの動作を生成する手法に関して多くの研究が行われている（例えば文献 [1]）．それに対して，本稿ではロボットアームの初期姿勢と目標姿勢が与えられているという条件の下で，ロボットアームが障害物を避けながら初期姿勢から目標姿勢へ到達する軌道を導出する問題に議論を絞り，この問題に関する最適化手法について議論する．このような問題は80 年代より解かれているクラシカルな研究である．例えばShiller ら [2] はロボットアームの最短時間動作計画を空間軌道を計画する問題と，軌道に沿った動作の時間軌道を計画する問題に分離することで解く手法を提案した．しかしながら，この手法においては障害物の形状を陽に与える必要があったため，複雑な形状をした環境モデルの問題に適用するのは非常に困難であった．その後，動作計画手法としてPRM （Probabilistic Roadmap Method）やRRT （Rapidly-Exploring Random Tree）などのランダムサンプリングに基づく手法 [3, 4] の有効性が認められて広く用いられるようになると，これらの手法のPost Processor として軌道長を短くする操作が行われるようになった [5, 6, 7, 8]．さらに，近年最適化手法をより直接的に動作計画のアルゴリズムの中に組み込むことで，評価関数を最適化するような軌道を導出する手法が提案されている．特に，RRT など従来の手法を改良することによる最適化手法 [9, 10] や関数最適化に基づく手法 [11, 12, 13, 14, 15] などが注目を集めている．本稿では，これらの手法を紹介し，また関連した筆者らの研究も同時に紹介する．

なお，例えばコンフィグレーション空間においてロボットアームの軌道の長さを最小化する場合，状態変数がSE(2) やSE(3) を含むと，最小化の定義自体が不明確になる [3]．本稿においては，コンフィグレーション空間C はC ⊂Rⁿ として定義される場合を考える．

2 Post Processor としての最適化

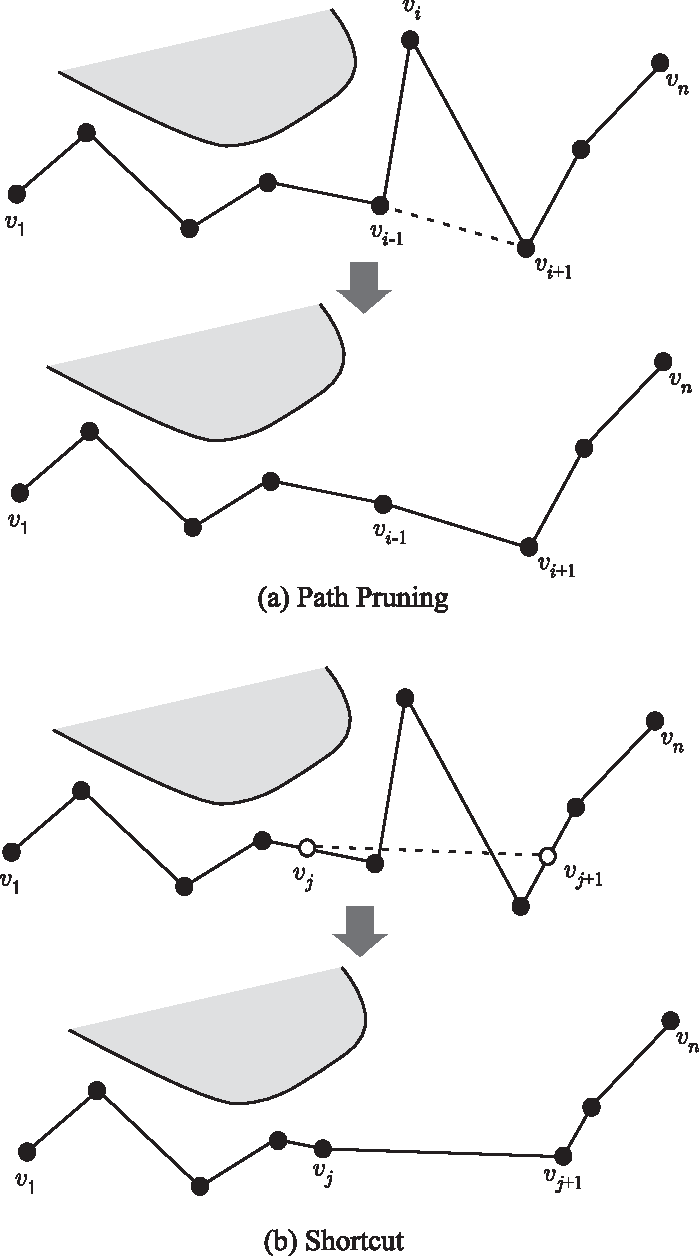
まず，何らかの動作計画手法により，ロボットアームが障害物を避けながら初期姿勢から目標姿勢へ到達する軌道が与えられていると仮定し，この軌道に対するPost Processor としての最適化手法について議論する．ここで，軌道はロボットのコンフィグレーションから構成されるノードと，このノードを直線で繋ぐパスにより構成される場合を考える．PRM やRRT は，このような軌道を出力することが可能であるが，これらのプランナによって生成される軌道は，通常不必要な迂回を多く含んでおり，この軌道を実行することで得られるロボットの動作はぎくしゃくしたものになる．また，これらの手法で得られた軌道は何らかの評価関数を最適化するものではないということが知られている [9]．そこで，PRM やRRT で得られた軌道の長さを短くすることを目的として，Path Pruning やShortcut と呼ばれる手法が広く用いられている [6, 5, 7, 8]．この概要をFig. 1に示す．ロボットの動作軌道がノードのリスト, v₁,,v_n ∈V とこれらを順番に直線で結ぶパスにより表現されている場合を考える．ここで，各ノードはロボットのコンフィグレーションq₁,,q_n によって定義される．

Path Pruning: ノードのリストv₁,,v_n ∈V からv_i を仮に取り除いたときに，v_i-1 とv_i+1 を結ぶパスに干渉が生じていないなら，実際にv_i を取り除く．この操作を繰り返し実行する．

Shortcut: ロボットの動作軌道上に二つの新たなノードv_j, v_j+1 をランダムに仮定する．これら二つのノードを結ぶパスに干渉が生じていないなら，v_j と v_j+1 の間に含まれるすべてのノードを取り除く．この操作を繰り返し実行する．

---

---

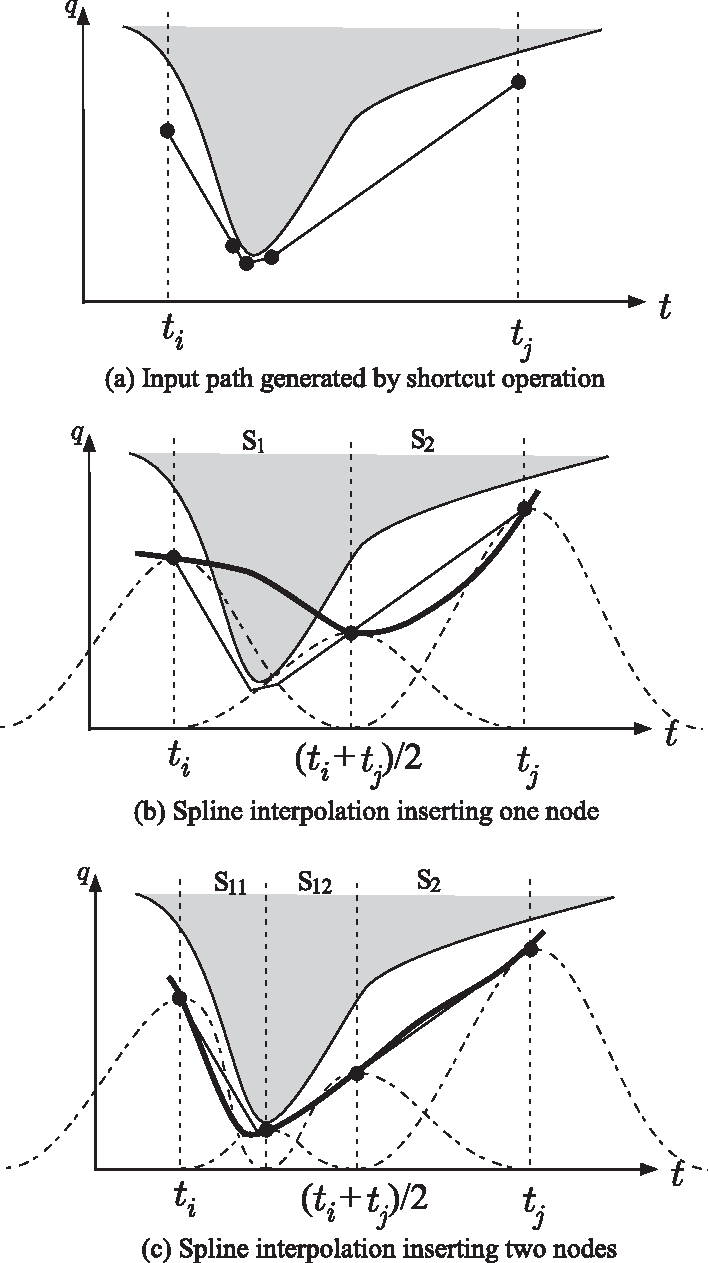
一般にPath Pruning と比較してShortcut のほうがより軌道長の短い軌道を求めることができる反面，軌道に含まれるノードの数が非常に多くなる場合がある．ここで，これらPost Processor によって得られる軌道は，その長さが最小のものであることは保証されていない．また，このアプローチによって得られる動作はノードごとにロボットが静止するものである．さらに，Post Processor への入力として与える軌道が，障害物を大きく迂回する軌道である場合は，Post Processor を実行しても，その軌道は本来軌道長が最短な軌道として得られるべき軌道からは大きく離れたものになる．また，これはPost Processor に限った問題ではないが，軌道長を短くする処理を行った軌道は，多くの場合障害物との干渉をぎりぎりで避けるものとなる．このような問題意識の下で，Post Processor に関して種々の研究が行われている．まず，より軌道長が短い軌道を得るために，自由度ごとにShortcut を行う手法が提案されている [5]．また，ノードごとにロボットが静止する問題に対しては，ノード間をスプライン関数で結ぶ手法が提案されている [7, 8]．特に，文献 [8] ではFig. 2に示すように，軌道上においてB-スプライン関数のノードをインクリメンタルに増やす手法を提案している．この手法を用いることにより，ヒューマノイドロボットが滑らかな動作で歩きながら障害物を避ける動作計画を実現している．また，障害物との距離を保ちながら障害物を避ける手法として，例えばGeraerts ら [5] はPath pruning やShortcut を実行した後のパスに対して，障害物からある程度の距離を確保する手法を提案している．

---

---

3 ランダムサンプリングに基づく手法の改良

次に，RRT やPRM の動作計画手法自体に，評価関数を最小化する作用を含めようという試みが行われており，その一つとしてRRT^* と呼ばれる手法を紹介する [9, 10]．この手法はAsymptotic Optimality，つまり最適解に収束することが保証されていることが特徴である．

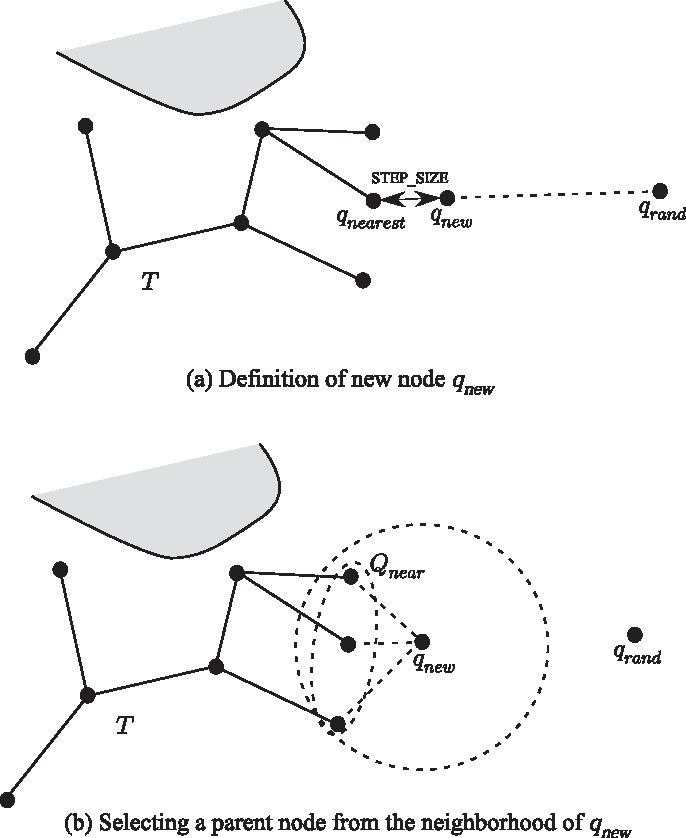
この手法の概要をFig. 3に示す．RRT^* では，通常のRRT と同様にコンフィグレーション空間内でノードV とエッジE から構成される木T = (V,E) をインクリメンタルに構築する．ランダムにコンフィグレーション q_rand を生成し，このq_rand から一番近い距離にあるT に含まれるノードを選択する．この一番近い距離にあるノードのコンフィグレーションをq_nearest とし，このq_rand とq_nearest を結ぶ直線上でq_nearst からSTEP_SIZE だけ離れた位置にq_new を仮定する．ここで，RRT ではq_new を新しいノードのコンフィグレーションとし，これをq_nearst に接続する．それに対してRRT^* ではq_new を中心とする球を仮定し，その球の内部に含まれるノードのコンフィグレーションの集合をQ_near と定義する．ここで，q_near ∈Q_near を q_new と直線により接続した場合のコストを以下により定義する．

ここで，Cost(q_near) はq_near に至ることに関するコストであり，c(Line(q_near,q_new)) は q_near からq_new に移動するのにかかるコストである．Q_near の要素の中で，このコストが最小になるものを選び，さらにノードを逆方向に辿った際のコストを考慮することで最終的にQ_near の要素の一つに対してq_new を接続する．文献 [9] では，RRT^* によりサンプル数を増やすに従って初期コンフィグレーションと目標コンフィグレーションを結ぶ軌道が最短距離の軌道に近づく様子が示されている．つまり，本手法ではプランナによって最初に得られる軌道が最適な軌道という訳ではない．また，文献 [10] では，RRT^* を実時間軌道計画問題に適用している．

---

---

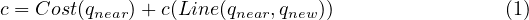
4 軌道最適化

次に，ロボットの軌道を陽に含んだ形で評価関数を定義し，この評価関数に対して関数空間において勾配を求めることで，評価関数を最小化するロボットの軌道を求める試みが行われている [12, 13, 14]．本章では，このような試みとしてCHOMP （Covariant Hamiltonian Optimization for Motion Planning）[12, 13] を紹介する．ここで，この手法の特徴は，従来から提案されている軌道を仮想的なバネ質量系でモデル化するElastic Strips Planning [11] などとは異なり，最初に与える軌道に干渉が生じていたとしても，最終的には干渉が生じていない軌道が得られる点である．つまり，最初に与える軌道としては，例えばロボットの初期姿勢と目標姿勢を直線軌道で結んだものを与えることができる．

CHOMP では，ロボットの軌道をξ: [0,1] →C ∈Rⁿ のような時間に関して正規化した滑らかな関数として定義し，動作の滑らかさの指標と障害物を避けることに関する指標を足し合わせた以下のような評価指標を最小化する．

ここで，λはF_smooth(ξ) に対する重みを表す．また，各評価指標は以下のように定義される．

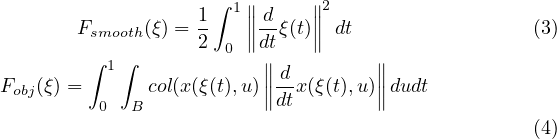
ここで，B ∈R³ はロボットの表面上の点集合であり，x : C ×B →R³ はロボットのコンフィグレーション q とロボット上の点u ∈B の順運動学マッピングである．さらに，col : R³ →R は干渉していない場合は距離，干渉している場合は干渉の深さに応じて値が変化する関数である．次に，この評価関数の勾配を求め，最急降下法により干渉を避ける滑らかな軌道を求めている．ここで，距離計算のコストを下げるため，ロボットのリンクを直方体，球，あるいは楕円体のような単純な形状の集合体としてモデル化している．また，局所最小解から抜け出すために，HMC （Hamiltonian Monte Carlo）法を用いている．この手法を用いることで，論文では7 自由度マニピュレータや4 足歩行ロボットの動作計画が実現できることを示している [13]．ここで，Ramirez ら [15] はCHOMP を応用することで，柔軟なリング状の部品を円柱に組み付けるための動作計画を行っている．この手法では，対象物の柔軟性を考慮したマニピュレーションが式（2）の評価関数に柔軟性を考慮した項を追加するだけで実現されている．

なお，このような関数最適化に基づくアプローチはROS （Robot Operating System）上で使えるソフトウェアパッケージとして提供されている [16]．近年，このようなアプローチを使った研究が増えてきている背景には，ROS に対応したソフトウェアパッケージが用意されていることがあると考えられる．

5 その他の事例

本稿では，ロボットの初期コンフィグレーションと目標コンフィグレーションが与えられている条件下で，評価関数を最適化しつつ障害物を避ける動作を計画する問題に絞って最近の事例を紹介している．本章では，上記問題に厳密には当てはまらないが関連する研究事例をいくつか紹介する．

まず，現在のコンフィグレーションが与えられているという条件下で，インクリメンタルに障害物を避けるロボットの動作を生成する研究が近年多く行われている [17, 18, 19]．また，ヒューマノイドロボットの初期手先位置と目標手先位置が与えられている条件下で評価関数を最適化する全身の動作を計画する研究が行われている [20]．さらに，障害物を避けるという条件を含めないのであれば，初期コンフィグレーションと目標コンフィグレーションを結ぶ最適軌道に関して従来から多くの研究が行われている（例えば文献 [21])．

6 結言

本稿では，ロボットの動作計画における最適化について議論した．特に，RRT, PRM などランダムサンプリングに基づく動作計画法のPost Processor としての最適化手法，ランダムサンプリングに基づく動作計画法自体の改良による最適化手法，ならびに関数最適化による動作計画法の三つを主に紹介した．

本稿によって，ロボットの軌道計画の研究分野が着実に進歩を遂げていることがお分かりいただけたのではないかと思う．ロボットが実時間で障害物を厳密に避けつつ，最適な軌道で初期姿勢から目標姿勢へと到達することができるアルゴリズムも，もうすぐ開発されるのではないかと期待させられる．本稿が，ロボット学会においてロボットの動作を生成することに関する研究を行っている研究者の動作計画の研究に対するモチベーションを高めることに寄与すると幸いである．

謝辞

本稿を作成するにあたり，平素より議論を行っている産業技術総合研究所のRamirez Ixchel 氏，吉田英一氏，九州大学の辻徳生氏，ならびにタスクビジョン研究グループのメンバーに感謝します．

References